Cara-cara Proyeksi yang digunakan

1. Gambar Proyeksi

Untuk menyajikan sebuah benda tiga dimensi pada sebuah bidang dua dimensi dipergunakan cara proyeksi.

Jika sebuah benda dilihat dari sebuah titik penglihatan O, seperti gambar 4.1 maka proyeksi dari benda ini pada bidang proyeksi P disebut proyeksi perpspektif dan gambarnya disebut gambar perspektif

Jika titik penglihatannya berada di tak terhingga, maka garis-garis proyeksi ( garis-garis penglihatan) menjadi garis sejajar, seperti pada gambar 4.2 . Proyeksi ini disebut proyeksi sejajar

Sedangkan proyeksi sejajar dibagi dua yaitu :

Proyeksi orthogonal, bila garis-garis proyeksi tegak lurus pada bidang proyeksi P

Proyeksi miring, bila garis-garis proyeksi membuat sudut dengan bidang proyeksi P

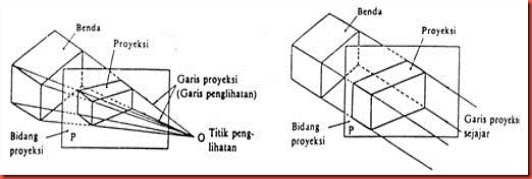
Gambar 4.1. Proyeksi Perspektif Gambar 4.2. Proyeksi Sejajar

2. Proyeksi Aksonometri 

   ( sejajar yang tegak lurus)

Jika sebuah benda disajikan dalam proyeksi orthogonal dan salah satu bidang sisinya frontal ( sejajar bidang proyeksi) seperti tampak pada gambar 4.3a, hanya sebuah bidang saja yang tergambar pada bidang proyeksi, maka tiga muka dari benda itu akan terlihat serentak, dan gambar demikian memberi bentuk benda seperti sebenarnya( mudah dimengerti/dipahami bentuk bendanya) gambar 4.3b. Cara demikian disebut proyeksi aksonometri. Tiga bentuk proyeksi aksonometri adalah isometric, dimetri dan trimetric.

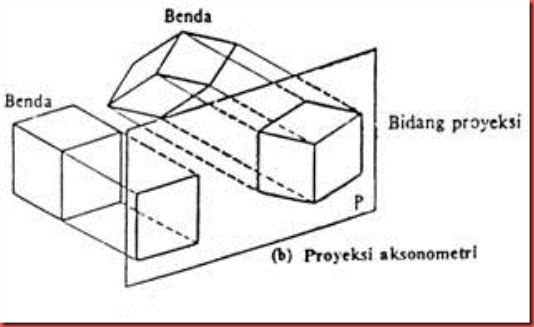
Gambar 4.3. Proyeksi Orthogonal

1. Proyeksi Isometri

Sebagai contoh diambil sebuah kubus. Pertama-tama kubus ini diletakkan seperti pada gambar 4.4a. Kemudian kubus ini dimiringkan sehingga diagonal benda berdiri tegak lurus bidang vertical ( bidang proyeksi). Sudut antara bidang bawah kubus dan bidang horizontal menjadi 35^o 16' Gambar 4.4b Jika kubus ini diproyeksikan pada bidang proyeksi akan menunjukkan ketiga bidang dari kubus . Dalam gambar proyeksi ini rusuk-rusuknya AB, AD dan AE ketiga-tiganya sama panjang dan saling berpotongan pada sudut yang sama pula, yaitu 120^o. Pada gambar 4.4c diperlihatkan skala perpendekan dari rusuk-rusuknya pada gambar proyeksi, yaitu 0,82 dari panjang rusuk sebenarnya. Proyeksi demikian disebut proyeksi isometric

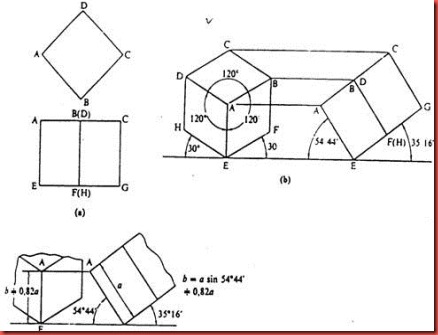
Gambar 4.4 Proyeksi isometri

2. Proyeksi dimetri

Disebut proyeksi dimetri, bila skala perpendekan dari dua rusuk dan dua sudut dari ketiga sudut yang dibentuk oleh ketiga rusuk yang berpotongan pada satu titik adalah sama

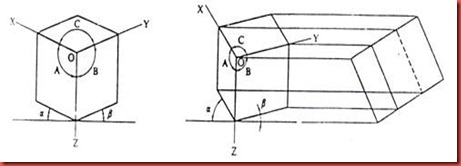
Gambar 4.5 dimetri Gambar 4.6. Proyeksi trimetri

3. Proyeksi trimetri

Proyeksi trimetric, bila skala perpendekan dari ketiga rusuk dan tiga sudut titik sama lihat gambar 4.6
Harga-harga dari sudut dan skala perpendekan dari proyeksi aksonometri yang khusus terdapat pada table dibawah ini
Tabel Sudut Proyeksi dan skala perpendekan

Cara Proyeksi	Sudut Proyeksi (o)	Skala Perpendekan
α	β	Sumbu x	Sumbu y	Sumbu z
Proyeksi Isometri	30	30	82	82	82
Proyeksi Dimetri	15 35 40	15 35 10	73 86 54	73 86 92	96 71 92
Proyeksi Aksonometri	20 30 30 35 45	10 15 20 25 15	64 65 72 77 65	83 86 83 85 92	97 92 89 83 86

3. Gambar Isometri

Orang lebih menyenangi gambar isometric, karena gambar isometric dapat menyajikan benda dengan tepat, dan memerlukan waktu yang lebih singkat dibandingkan dengan cara proyeksi yang lain. Berikut contoh gambar isometric dengan berbagai kedudukan sumbu utama Gambar 4.7. Kedudukan sumbu isometric dipilih sesuai tujuan dan hasil yang akan memberikan gambar yang paling jelas.

Gambar 4.7 Kedudukan sumbu-sumbu isometric

Gambar isometric dari sebuah 

benda dengan sebuah bidang miring

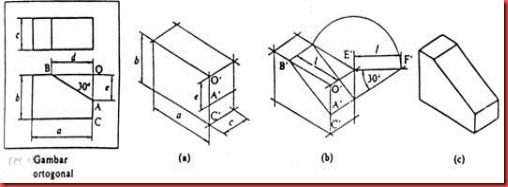
Gambar 4.8

4. Proyeksi Miring

Gambar 4.9. Perbandingan beberapa jenis proyeksi miring proyeksinya miring terhadap bidang proyeksi. Pada proyeksi ini benda dapat diletakkan sesukanya tetapi biasanya permukaan depannya diletakkan frontal terhadap bidang proyeksi vertical. Dengan demikian bentuk permukaan depan tergambar seperti sebenarnya, yang juga terdapat pada proyeksi orthogonal. Sudut yang menggambarkan kedalamannya biasanya sudut 30, 45 dan 60 derajat terhadap sumbu horizontal yang disebut juga sudut proyeksi. Pada rusuk yang miring ini bila dipakai skala perpendekan= 0,5 dan sudut proyeksi 45^o memberikan bentuk gambar yang jelas dan mudah dipahami seperti sebenarnya dan penggambarannya agak mudah.

Gambar 4.10 memperlihatkan gambar sebuah benda dalam proyeksi isometric dan proyeksi miring dapat dipakai sebagai perbandingan

Gambar 4.10 Perbandingan Gambar isometric dan gambar Proyeksi Miring

Cara-cara Proyeksi yang digunakan

dalam gambar teknik

1. Dasar-dasar Proyeksi orthogonal

Untuk dapat memproyeksikan benda secara orthogonal ( tegak lurus) perlu kita pahami dasar-dasar proyeksi orthogonal. Benda tidaj lain dibatasi oleh bidang dan garis potong dari bidang bidang tersebut. Untuk dapat memproyeksikan benda tersebut, kita harus dapat memproyeksikan bidang dan garis. Untuk memproyeksikan bidang sama dengan memproyeksikan 2 garis yang berpotongan pada bidang tersebut. Sedang untuk memproyeksikan garis adalah sama dengan memproyeksikan dua titik yang tidak berimpit pada garis tersebut. Berikut contoh proyeksi titik pada bidang proyeksi gambar 5.1a proyeksi garis PG pada bidang proyeksi, masing-masing untuk PQ // bidang proyeksi. Gambar 5.1b, PQ terletak sebarang terhadap bidang proyeksi, gambar 5.1.c dan PQ tegak lurus bidang proyeksi gambar 5.1d sedang pada gambar 5.2 menunjukkan urut-urutan proyeksi orthogonal dari suatu benda pada satu bidang proyeksi.

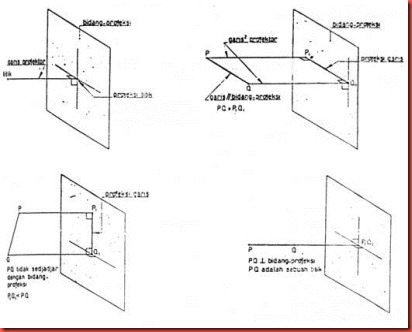
Gambar 5.1. Proyeksi Orthogonal dari titik dan garis

Gambar 5.2. Proyeksi Orthogonal dari benda

2. Proyeksi Orthogonal dalam gambar teknik

Dalam gambar teknik kita mengenal dua macam proyeksi, yaitu

a. Proyeksi Eropa atau proyeksi sudut pertama dan

b. Proyeksi Amerika atau proyeksi sudut ketiga

a. Proyeksi Eropa

Ketentuan dari proyeksi eropa, benda terletak antara pengamat dan bidang proyeksi. Cara memproyeksikan :

Benda yang akan kita proyeksikan harus kita rencanakan mana yang kita anggap sebagai pandangan depan, misalnya A adalah pandangan depan, B adalah pandangan atas, C adalah pandangan kiri, D Pandangan Kanan, E pandangan bawah, dan F pandangan Belakang ditunjukkan oleh anak panah pada gambar 5.3a. Ini menunjukkan dari arah mana pengamat/ orang akan memproyeksikan.

Kemudian benda kita masukkan kedalam kubus yang transparan ( tembus pandang) gambar 5.3b. Dengan kekentuan dari proyeksi eropa di atas, maka gambar proyeksi pandangan depan ( A) ada dibidang sisi belakang dari kubus, gambar proyeksi pandangan atas (B) ada di sisi bawah, gambar proyeksi pandangan kiri ( C) ada di sisi kanan, Gambar proyeksi pandangan kanan ( D) ada di sisi kiri, GAmbar proyeksi pandangan bawah (E) ada dibidang sisi atas dan gambar proyeksi belakang ada dibidang sisi depan Gambar 5.3b

Kemudian sebagian dari rusuk-rusuk dari kubus tersebut kita potong dan bidang sisinya kita rebahkan kebidang belakang dari kubus, sehingga menjadi satubidang dengan gambar proyeksi pandangan depan.

Bila garis-garis rusuk kubus tersebut kita hilangkan, maka terlihat hasil proyeksi eropa seperti pada gambar 5.3d
Ciri-ciri dari hasil proyeksi eropa :

1. Pandangan atas terletak dibawah pandangan depan
2. Pandangan kiri terletak dikanan pandangan depan
3. Pandangan kiri terletak di kiri pandangan depan
4. Panfangan bawah terletak di atas pandangan depan

Gambar 5.4. Proyeksi Eropah atau Proyeksi Sudut Pertama

b. Proyeksi Amerika

Ketentuan dari proyeksi amerika , bidang proyeksi terletak antara pengamat dan benda. Cara memproyeksikannya : Benda yang akan kita proyeksikan kita ambil sama dengan benda yang diproyeksikan dengan cara eropa, gambar 5.3.a, termasuk arah memandangnya.

Kemudian benda kita masukkan dalam kubus yang transparan ( tembus pandang) gambar 5.4a. Dengan ketentuan dari proyeksi amerika di atas, maka gambar proyeksi pandangan Depan (A) ada dibidang sisi depan kubus, gambar proyeksi pandangan atas (B) ada di bidang atas, Pandangan sisi kiri (C) ada di sisi kiri, pandangan sisi kanan (D) ada di sisi kanan , pandangan bawah (E) ada di sisi bawah, pandangan sisi belakang (F) ada di belakang lihat gambar 5.4a

Kemudian sebagian dari rusuk-rusuk dari kubus tersebut kita potong dan bidang sisinya kita rebahkan kebidang belakang dari kubus, sehingga menjadi satubidang dengan gambar proyeksi pandangan depan.

Bila garis-garis rusuk kubus tersebut kita hilangkan, maka terlihat hasil proyeksi Amerika seperti pada gambar 5.4c
Ciri-ciri dari hasil proyeksi Amerika :

1. Pandangan atas terletak di atas pandangan depan
2. Pandangan kiri terletak dikiri pandangan depan
3. Pandangan kiri terletak di kanan pandangan depan
4. Panfangan bawah terletak di bawah pandangan depan

Gambar 5.4. Proyeksi Amerika atau Proyeksi sudut ketiga

Fungsi dan Sifat Gambar sebagai Gambar Teknik

Alat – alat Gambar dan Penggunaannya

Garis dan Huruf

1. Macam garis dan tebal garis

Didalam menggambar teknik bentuk dan tebal garis sesuai dengan penggunaanya seperti contoh dibawah ini ;

	Jenis		Macam Garis	Contoh-contoh Penggunaan
A		0,6 0,8	Garis tebal	1. Garis benda langsung terlihat 2. Garis tepi
B		0,1 0,2	Garis tipis	1. Garis penunjuk ukuran, garis Bantu, garis penunjuk 2. Garis arsir 3.Garis untuk Penampung yang diputar ditempat 4. Garis khayal yang terjadi dari perpotongan yang dibulatkan
C		0,1 0,2	Garis bebas tipis	1. Garis potong, yang menghilangkan sebagian benda 2. Garis batas antara bagian benda yang dipotong dan sebagian dalam pandangan
D		0,3 0,4	Garis sedang ( putus-putus)	Garis benda yang terhalang/tidak langsung terlihat
E		0,1 0,2	Garis tipis ( strip titik)	1. Garis sumbu 2. Garis potomg penampang

2. Huruf dan angka

Ciri-ciri yang perlu pada huruf dan angka dalam gambar teknik, ialah ; jelas dan seragam dalam ISO 3098/1-1974 diberikan contoh-contoh huruf dan angka, satu untuk huruf miring dan satu untuk huruf tegak, kedua-duanya boleh digunakan Pada gambar 3.3 dicontohkan untuk huruf dan angka yang miring
ABCDEFGHIJKLMNOPQRSTUVWXYZ
0123456789 ~!@#$%^&*()_+|
Bentuk Huruf Miring ISO
Ukuran huruf
Tinggi h dari huruf besar diambil sebagai dasar ukuran. Daerah standar tinggi huruf adalah sebagai berikut : 2,5;3,5;5;7;10; 14; dan 20 mm
Tinggi h ( huruf besar) dan c ( tinggi huruf kecil) tidak boleh kurang dari 2,5 mm. Bila terdapat gabungan antara huruf besar dan kecil, dengan huruf kecil setinggi 2,5 mm, maka h akan menjadi 3,5 mm
Tebal huruf d ditentukan oleh dua perbandingan standard d/h, yaitu antara d/h = 1/14 dan d/h = 1/10. Perbandingan yang dianjurkan untuk tinggi huruf-huruf kecil, jarak antara huruf-huruf, ruang minimum antara garis dasar dan jarak antara perbatasan-perbatasan diberikan pada table berikut :

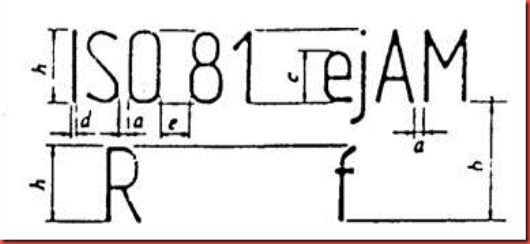
Huruf A ( d= h/14)

Sifat	Perbandingan	ukuran
Tinggi huruf h Tinggi huruf besar Tinggi huruf kecil c (tanpa tangkai dan kaki)	(14/14)h (10/14)h	2,5	3,5 2,5	5 3,5	7 5	10 7	14 10	20 14
Jarak antar huruf a Jarak minimum antara garis b Jarak minimum antara perkataan e	(2/14)h (20/14)h (6/14)h	0,35 3,5 1,05	0,5 5 1,5	0,7 7 2,1	1 10 3	1,4 14 4,2	2 20 6	2,8 28 8,4
Tebal huruf d	(1/14)h	0,18	0,25	0,35	0,5	0,7	1	1,4

Catatan : Jarak antara dua huruf a boleh dikurangi setengahnya, bila mana ini memberi efek visual yang lebih baik : seperti misalnya LA,TV dsb, d,h,I,a sama dengan tebal huruf d

Huruf B ( d= h/10)

Sifat	Perbandingan	ukuran
Tinggi huruf h Tinggi huruf besar Tinggi huruf kecil c (tanpa tangkai dan kaki)	(10/10)h (7/10)h	2,5	3,5 2,5	5 3,5	7 5	10 7	14 10	20 14
Jarak antar huruf a Jarak minimum antara garis b Jarak minimum antara perkataan e	(2/10)h (14/10)h (6/10)h	0,5 3,5 1,5	0,7 5 2,1	1 7 3	1,4 10 4,2	2 14 6	2,8 20 8,4	4 28 1,2
Tebal huruf d	(1/10)h	0,25	0,35	0,5	0,7	1	1,4	2

Catatan : Jarak antara dua huruf a boleh dikurangi setengahnya, bila mana ini memberi efek visual yang lebih baik : sepert

Categories: Materi